Daten visualisieren mit ggplot2

Niels Schwab
RLab - Skriptbasierte modulare Umweltstatistik (Universitätskolleg 2.0)
Universität Hamburg
RLab-Impressum
Gefördert im Rahmen des „Lehrlabors“ im Universitätskolleg 2.0 aus Mitteln des BMBF (01PL17033)

Dieses Digitale Skript von Niels Schwab, Universitätskolleg 2.0 / Lehrlabor, Universität Hamburg, ist lizenziert unter einer Creative Commons Namensnennung - Weitergabe unter gleichen Bedingungen 4.0 International Lizenz.
elearn.js Template
Universität Hamburg
Das elearn.js Template von Universität Hamburg ist lizenziert unter einer Creative Commons Namensnennung - Weitergabe unter gleichen Bedingungen 4.0 International Lizenz
Ziel
Dieses Digitale Skript stellt das ggplot2-Konzept zum Visualisieren von Daten vor und beinhaltet Hintergrundinfos zum R-Package ggplot2. Ziel ist, die Nutzung der Funktionen des ggplot2-Packages verständlich(er) zu machen und zu erleichtern. Damit ergänzt dieses Digitale Skript den gleichnamigen RLab-Kurs.
In diesem Digitalen Skript wird nicht gezeigt,
wie sich "auf die Schnelle" Abbildungen mit ggplot2 erstellen lassen - dabei kann aber der gleichnamige RLab-Kurs unterstützen.
Der RLab-Kurs kann auch ohne die Lektüre dieses Digitalen Skripts bearbeitet werden, wenn kein Anspruch besteht, alles bis ins letzte Detail zu verstehen.
Voraussetzungen
Um dieses Skript gut zu verstehen, solltest Du grundlegende R-Kenntnisse besitzen. Wenn Du beim Lesen dieses Skripts ggplot2-Funktionalitäten gleich in R ausprobieren möchtest, solltest Du R und RStudio installiert haben. Am besten öffnest Du parallel RStudio, so dass Du die im Folgenden vorgestellten Funktionalitäten direkt ausprobieren kannst. Das Digitale Skript kannst Du auch auf einem Smartphone oder Tablet lesen.
Fragen oder Anmerkungen?
Für Anregungen und Kommentare zur Verbesserung dieses Digitalen Skripts ist das RLab-Team immer dankbar! Du kannst auch Fragen zu den Inhalten stellen! Nutze für all das gerne die Kommentar-Funktion!
Das "grammar of graphics"-Konzept
Das Visualisieren quantitativer Daten und Analyseergebnisse ist für Ergebnispräsentationen unabdingbar. Die Erstellung solcher Grafiken kann viel Aufwand bedeuten - manchmal mehr als die Analyse selbst erfordert. Standardisierte Verfahren und Regeln zur Erstellung von Abbildungen können die Effizienz dabei erhöhen.
,,Grammar of Graphics" (Wilkinson 2005) steht für eine Grammatik, im weitesten Sinne also eine Sammlung grundlegender Prinzipien oder Regeln, für die Beschreibung und Erstellung statistischer Grafiken. Mit ,,grammar of graphics" kann über die ausschließliche Benennung von Abbildungen z.B. als Streudiagramm, hinausgegangen werden. Die Gesamtheit einzelner Merkmale und Bestandteile, die statistischen Abbildungen zugrunde liegen, können mit ihr beschrieben werden. Das grammar of graphics-Konzept, die in Wilkinson (2005) publizierten theoretischen und mathematischen Grundlagen, sind in zahlreiche Programmbibliotheken eingegangen. Auch die "Layered Grammar of Graphics" (Wickham 2010) und das R-Package ggplot2 basieren darauf. Die theoretischen und mathematischen Grundlagen sind bei der praktischen Arbeit mit den ggplot2-Funktionen immer im Hintergrund dabei, es reicht aber ein strak vereinfachtes, prinzipielles Verständnis, um sie erfolgreich anwenden zu können. Kurz gesagt liegen im Vergleich zu einfachen Funktionen (zum Beispiel plot()), die Daten ,,nur" 1:1 aufs Papier bzw. den Bildschirm übertragen, die Stärken der ,,(Layered) Grammar of Grapohics" und der ggplot2-Funktionen im Umformen und -ordnen sowie Transformieren der einer Abbildung zugrunde liegenden Daten sowie dem Zusammenstellen einer Abbildung aus einzelnen Elementen.
Die ,,layered grammar of graphics" und ihre Implementierung in ggplot2
Die auf der ,,Grammar of Graphics" (Wilkinson 2005) basierende ,,Layered Grammar of Graphics" (Wickham 2010) beschreibt eine Ebenen- (Schichten-; engl. ,,layer") basierte Herangehensweise beim Erstellen von Grafiken. Einzelne Ebenen oder Schichten mit verschiedenen Grafikkomponenten werden nach und nach zusammengefügt, um die finale Abbildung zu erhalten. Dabei können die "Bausteine" unabhängig voneinander definiert (und später auch geändert!) und kombiniert werden, um nahezu jede Art von Grafikdarstellung zu erstellen.
Bestandteile der "layered grammar of graphics" sind (kompakt & abstrakt dargestellt - anschaulicher wird es auf den folgenden Seiten):
- Daten
- Zuordnungen von in den Daten enthaltenen Variablen zu ,,ästhetischen Eigenschaften" (Designs)
- eine oder mehrere Ebenen, die jeweils
- ein geometrisches Objekt,
- eine statistische Transformation bzw. Berechnung ästhetischer Eigenschaften und
- eine Positionseinstellung besitzen sowie
- optional einen Datensatz und eine Zuordnung der Variable(n) zu ästhetischen Eigenschaften.
- eine Skala für jede verwendete ästhetische Zuordnung
- ein Koordinatensystem
- eine Facettenspezifikation (Angabe, ob und wie Teilstichproben nebeneinander dargestellt werden)
Bei der praktischen Arbeit mit ggplot2 besitzen viele der Bestandteile Standardeinstellungen, so dass nicht alle immer angegeben werden müssen. Dadurch ist es möglich, einfache Abbildungen mit wenigen Code-Elementen einfacherer, als es aus der obigen Auflistung erscheint, zu erstellen.
Die Ebenen sind besonders wichtig, da sie die physische Darstellung der Daten bestimmen, wobei die Kombination aus statistischer Transformation (in ggplot2 "stat…()") und geometrischem Objekt (in ggplot2 "geom…()") viele bekannte Grafiken wie Streudiagramm, Histogramm, Konturdiagramm usw. definiert.
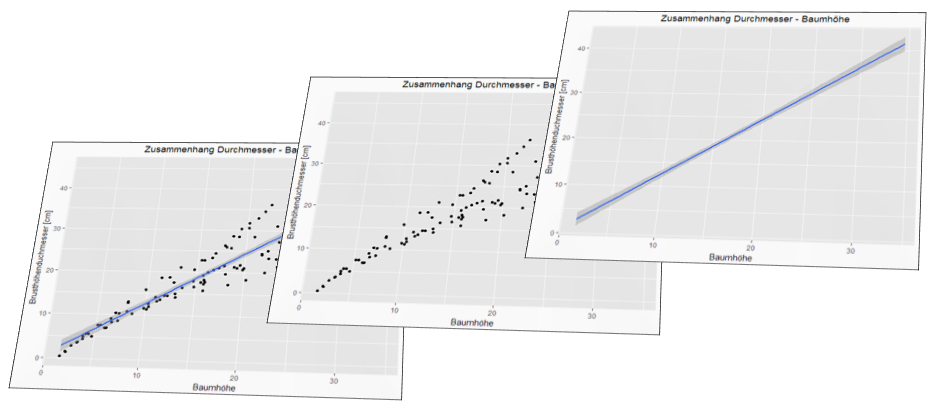
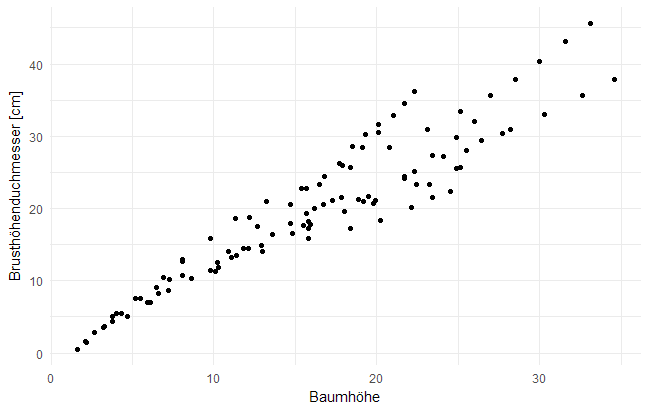
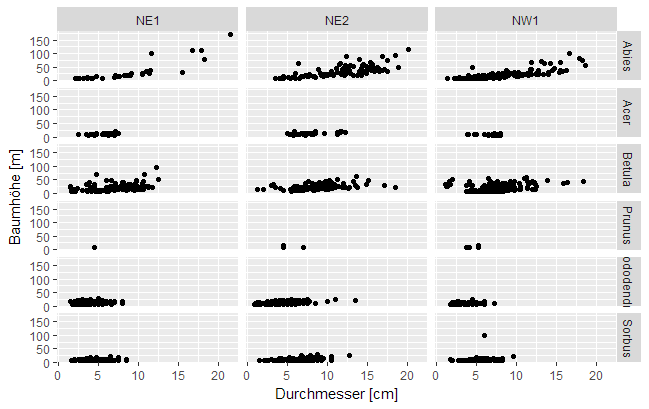
Abb. 1: Das Streudiagramm mit Regressionsgerade (unten) setzt sich aus einem ggplot2-Layer mit Streudiagramm (Mitte) und einem ggplot2-Layer mit der Regressionsgeraden (inkl. Konfidenzintervall) (oben) zusammen.
Die "layered grammar of graphics" bzw. ggplot2 sind haben eine Vielzahl von Vorteilen gegenüber anderen Methoden, Abbildungen zu erstellen.
- Eine Abbildung kann einfacher wiederholt aktualisiert werden, indem jeweils nur eine einzelne Funktion geändert oder hinzugefügt wird.
- Die übergeordneten Aspekte eines Plots sind gesondert enthalten und können somit leicht geändert werden. Damit steht ein Rahmen zum Nachdenken über Grafiken zur Verfügung, der die Distanz zwischen Vorstellung und der Abbildung auf dem Papier oder Bildschirm verkürzen kann.
- Die Entwicklung und Nutzung von speziellen, an ein bestimmtes Problem angepassten Grafiken im Gegensatz zu üblichen einfachen Grafiktypen wie zum Beispiel Streu- oder Balkendiagrammen ist vereinfacht.
Die folgenden Seiten dieses Digitalen Skripts gehen detailliert und anschaulich auf die einzelnen Bestandteile ein.
Grundstruktur einer ggplot2-Funktion
Jede ggplot2-Funktion hat mindestens drei Hauptbestandteile:
- Ein Datensatz
- Ästhetische Zuordnungen, die angeben, wie den Daten visuelle Eigenschaften zugeordnet werden (zum Beispiel die Zuordnung einer Variable des Datensatzes zu x- oder y-Achse oder zu Farben für verschiedene Variablenwerte).
- Mindestens ein ,,Layer" (eine Ebene oder Schicht der Abbildung; siehe folgendes Kapitel), der beschreibt, wie die Beobachtungen aus dem Datensatz angezeigt werden sollen (zum Beispiel als Punkte, Linien oder Boxplots).
Der Datensatz und die ästhetische Zuordnung werden innerhalb der ggplot()-Funktion angegeben, der oder die Layer werden mit einen ,,+" hinzugefügt:
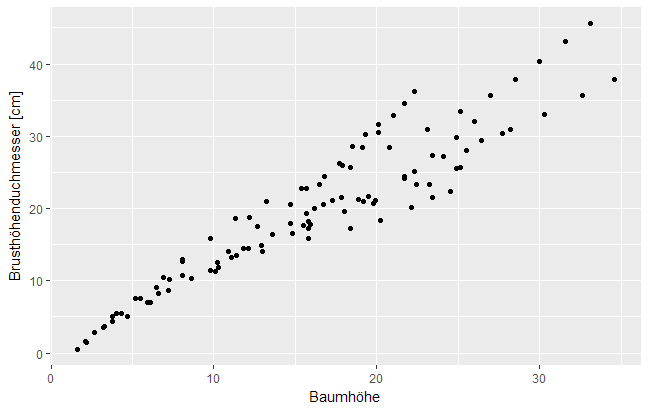
ggplot(gutten_sub, aes(x=height, y=dbh.cm)) + geom_point()
In diesem Beispiel werden die Variablen height und dbh.cm des Datensatzes gutten_sub x- bzw. y-Achse zugeordnet und als Punkte abgebildet. Weitere Layer, Bestandteile und Einstellungen können mit weiteren ,,+"-Zeichen hinzugefügt werden, um immer ausgeklügeltere Abbildungen zu erstellen. Einige dieser Bestandteile werden in den einzelnen Abschnitten dieses Digitalen Skripts vorgestellt.
Fragen oder Anmerkungen?
Für Anregungen und Kommentare zur Verbesserung dieses Digitalen Skripts ist das RLab-Team immer dankbar! Du kannst auch Fragen zu den Inhalten stellen! Nutze für all das gerne die Kommentar-Funktion!
Layer
- Daten und sog. ästhetische Zuordnungen,
- statistische Transformation,
- ein geometrisches Objekt und
- eine Positionseinstellung
bilden zusammen einen Layer (eine ,,Schicht") einer Abbildung.
Eine Abbildung kann mehrere Layer haben, zum Beispiel, wenn in ein Streudiagramm (Layer 1) mit einer Linie (Layer 2) versehen wird. Meistens haben alle Layer einer Abbildung etwas gemeinsam. Typischerweise sind sie verschiedene Ansichten derselben Daten, zum Beispiel ein Streudiagramm und eine Gerade einer linearen Regression, die ein Modell der Datenpunkte des Streudiagramms visualisiert.

Abb. 2: Das Streudiagramm mit Regressionsgerade (unten) setzt sich aus einem ggplot2-Layer mit Streudiagramm (Mitte) und einem ggplot2-Layer mit der Regressionsgeraden (inkl. Konfidenzintervall) (oben) zusammen.
Daten und Zuordnungen
Daten sind zwar das bedeutendste Element einer statistischen Abbildung, allerdings sind sie aus Sicht der ,,grammar of graphics" von den anderen Bestandteilen unabhängig. Eine Abbildung bzw. ihr ggplot2-Code kann auf verschiedene Daten angewendet werden. Daten machen aus einer abstrakten Grafikvorlage eine konkrete Grafik.
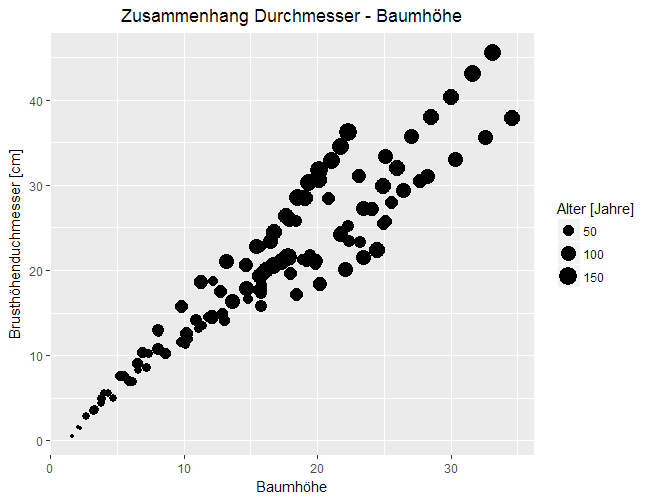
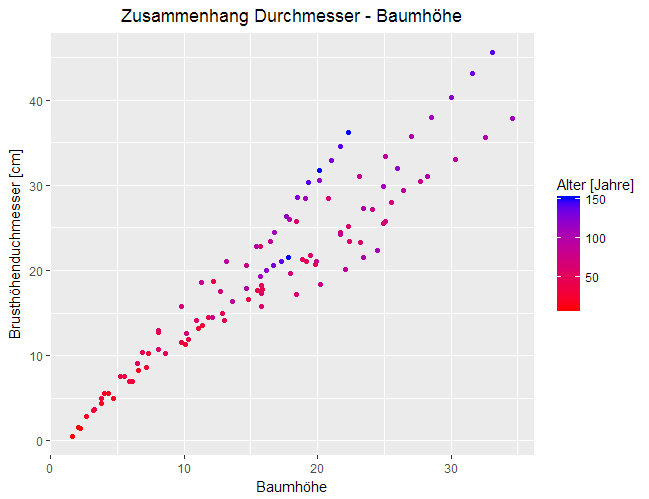
Im Zusammenhang mit den Daten werden auch Zuordnungen der Daten einzelner Variablen zu ,,ästhetischen Eigenschaften" (in ggplot2 "aes_…()") benötigt. Zum Beispiel kann die Variable ,,Baumhöhe" der x-Achse eines Koordinatensystems zugeordnet werden, die Variable ,,Brusthöhendurchmesser" der y-Achse und die Variable ,,Alter" der Größe der Punkte.
In ggplot2 werden diese Zuordnungen mit den sog. ,,scales" (in ggplot2 "scale_…()")definiert. ,,Scales" ordnen Werte des Datenraums Werten eines ästhetischen Raums, eines Designs zu. Durch ,,scales" werden Achsen oder Legenden erstellt, die eine inverse Zuordnung darstellen um das Ablesen der Datenwerte aus der Abbildung zu ermöglichen.
Fragen oder Anmerkungen?
Für Anregungen und Kommentare zur Verbesserung dieses Digitalen Skripts ist das RLab-Team immer dankbar! Du kannst auch Fragen zu den Inhalten stellen! Nutze für all das gerne die Kommentar-Funktion!
Statistische Transformation
Durch eine statistische Transformation (in ggplot2 "stat_…()") werden aus den Daten neue Werte für die Abbildung berechnet. Dabei werden die Daten in der Regel in irgendeiner Weise zusammengefasst. Es kann sich zum Beispiel um die Zusammenfassung von zweidimensionalen Beziehungen mit einem linearen Regressionsmodell handeln. Eine statistische Transformation kann auch neue Variablen zum Datensatz hinzufügen bzw. aus ihm Ableiten: Die Klasseneinteilung und das Zählen von Beobachtungen zur Erstellung eines Histogramms ist so ein Fall. Dabei nimmt die Funktion zur statistischen Transformation die Original-Daten als Input und erstellt als Output die numerische Beschreibung des Histogramms mit der Spezifikation der Klassen und Anzahl der Beobachtungen pro Klasse.
Folgende statistische Transformationen sind in ggplot2 vordefiniert:
| Statistische Transformation | Beschreibung der Funktion |
|---|---|
| bin | Einteilung kontinuierlicher Daten in Klassen und Zählen der Beobachtungen pro Klasse |
| boxplot | Berechnung der Parameter für eine Boxplot-Darstellung |
| contour | Berechnung von Konturlinien |
| density | eindimensionale Dichteschätzung |
| identity | Die Daten werden unverändert belassen, f(x) = x |
| jitter | Durch Addieren kleiner, zufälliger Werte sog. Jitter (,,Schwankung", ,,Flimmern") hinzufügen, um übereinander liegende Punkte sichtbar zu machen |
| Werte für einen Quantil-Quantil-Plot berechnen | |
| quantile | Quantil-Regressionsmodell |
| smooth | geglätteter, bedingter Erwartungswert von y bei gegebenem x |
| summary | Aggregieren von y-Werten für gegebene x-Werte |
| unique | Entfernen von doppelten Beobachtungen |
Fragen oder Anmerkungen?
Für Anregungen und Kommentare zur Verbesserung dieses Digitalen Skripts ist das RLab-Team immer dankbar! Du kannst auch Fragen zu den Inhalten stellen! Nutze für all das gerne die Kommentar-Funktion!
Geometrische Objekte
Geometrische Objekte (in ggplot2 "geom_…()") stellen dar, was auf der Abbldung zu sehen ist: Punkte, Linien, Polygone usw. Sie lassen sich nach ihrer Dimensionalität einteilen:
Trotz der vermeintlichen Eindeutigkeit, die sich aus dieser Beschreibung ergibt, sind geometrische Objekte abstrakte Bestandteile einer Abbildung und können in unterschiedlicher Weise wiedergegeben werden (siehe Slideshow).
Fragen oder Anmerkungen?
Für Anregungen und Kommentare zur Verbesserung dieses Digitalen Skripts ist das RLab-Team immer dankbar! Du kannst auch Fragen zu den Inhalten stellen! Nutze für all das gerne die Kommentar-Funktion!
Zusammenhang zwischen statistischer Transformation und geometrischem Objekt
Sowohl stat…()- als auch geom…()-Funktionen kombinieren ein geometrisches Objekt mit einer statistischen Transformation, um einen Layer zu erstellen. Das bedeutet, dass
stat_bin(geom="bar")
das gleiche wie
geom_bar(stat="bin")
ergibt.
Ein geometrisches Objekt beinhaltet immer eine statistische Transformation. Wenn diese nicht explizit angegeben wird, verwendet ggplot2 eine Standardeinstellung. Welche das ist, geht aus der Hilfe zur jeweiligen geom_…()-Funktion hervor. Dort ist im Abschnitt ,,Computed Variables" auch angegeben, welche neuen Variablen durch die Transformation (bei Standardeinstellung) hinzukommen.
Häufig ,,arbeitet" die Funktion zur statistischen Transformation also mit der Standardeinstellung im Hintergrund und braucht kaum beachtet zu werden. Es kann aber dennoch aus verschiedenen Gründen Sinn machen oder erforderlich sein, sich nicht auf die Standardeinstellung der statistischen Transformation des geometrischen Objekts zu verlassen und diese zu überschreiben.
Positionseinstellung
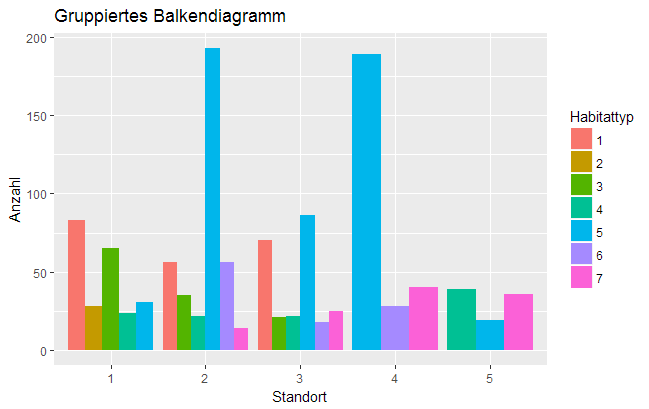
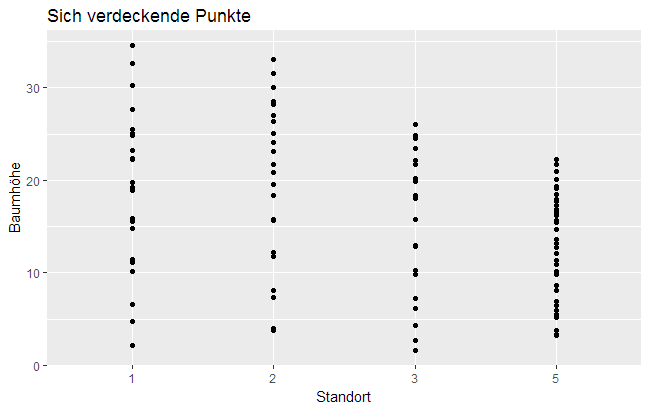
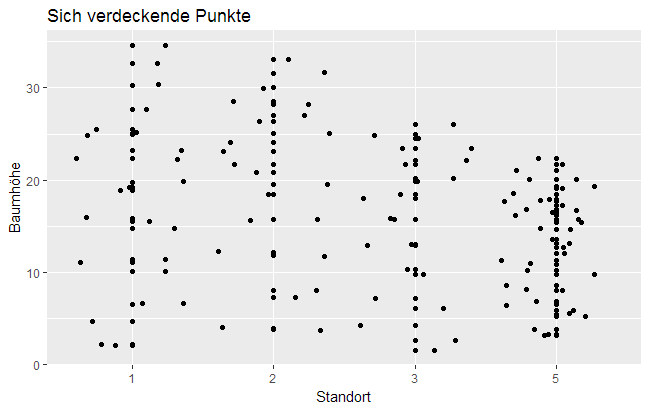
Manchmal ist es erforderlich, die Position von Elementen (in ggplot2 "position_…()")in einer Abbildung zu justieren, damit sich Daten(punkte) nicht gegenseitig verdecken. Dies ist am häufigsten bei Barplots der Fall, bei denen das Stapeln oder nebeneinander Platzieren der Balken Abhilfe schafft. Auch bei Streudiagrammen mit wenigen eindeutigen x- und y-Werten (also vielen Punkten an gleicher Stelle) kann eine Positionseinstellung, in diesem Fall das Hinzufügen eines ,,Jitter", das Addieren kleiner, zufälliger Werte, Sinn machen.
Fragen oder Anmerkungen?
Für Anregungen und Kommentare zur Verbesserung dieses Digitalen Skripts ist das RLab-Team immer dankbar! Du kannst auch Fragen zu den Inhalten stellen! Nutze für all das gerne die Kommentar-Funktion!
Koordinatensystem
Neben dem Layer oder den Layern ist das Koordinatensystem (in ggplot2 "coord_…()") ein weiterer Bestandteil einer ggplot2-Abbildung. Das Koordinatensystem weist den Objekten ihre Position auf der Ebene der Abbildung zu. Es stellt auch Achsen und Gitternetzlinien zur Verfügung, um die Lesbarkeit des Diagramms zu erreichen. Die Position wird häufig mittels zweier Koordinaten (x,y) zugewiesen, es kann sich aber prinzipiell um jegliche Anzahl an Koordinaten handeln.
Für zwei Dimensionen ist das Kartesische Koordinatensystem das am häufigsten verwendete, Polarkoordinaten oder verschiedene Kartenprojektionen werden seltener verwendet. Für höhere Dimensionen stehen Parallelkoordinaten (eine projektive Geometrie), Mosaik-Plots (ein hierarchisches Koordinatensystem) und lineare Projektionen in die Ebene zur Verfügung.
Die Einstellung des Koordinatensystems beeinflusst alle Positionsvariablen gleichzeitig und unterscheidet sich von den ,,Scales" dadurch, dass es auch die Darstellung der geometrischen Objekte verändert. Zum Beispiel sieht das geometrische Objekt ,,Balkendiagramm" in einem Polarkoordinatensystem aus wie Segmente eines Kreises. Außerdem wird das ,,Scaling" vor der statistischen Transformation durchgeführt, wohingegen die Koordinatentransformationen hinterher erfolgen.
Themes
Themes kontrollieren die Anzeige aller Bestandteile der Abbildung, die nicht durch Daten definiert werden. Dazu zählen zum Bespiel Schriftgröße oder Hintergrundfarbe. ggplot2 stellt eine Reihe an kompletten Themes zur Verfügung, die verschiedene ,,Stile", z.B. ,,dark", ,,light" oder ,,minimal", repräsentieren. Es ist nicht erforderlich, ein Theme ausdrücklich anzugeben, ggplot2 verwendet dann das Standard-Theme ,,themegray()" (identisch mit ,,themegrey()"). Einzelne Theme-Elemente, zum Beispiel die Schriftgröße eines Abbildungstitels können mit der Funktion "theme()" verändert werden.
Mit dem cowplot-Package lassen sich Einzelgrafiken zusammensetzen und ein besonderes, "publikationsbereites" Theme nutzen.
Fragen oder Anmerkungen?
Für Anregungen und Kommentare zur Verbesserung dieses Digitalen Skripts ist das RLab-Team immer dankbar! Du kannst auch Fragen zu den Inhalten stellen! Nutze für all das gerne die Kommentar-Funktion!
Facetting
Das sogenannte ,,Faceting" (in ggplot2 "facet_…()") bewirkt, dass die Daten in Untergruppen (sog. ,,Subsets") geteilt werden und als kleine Abbildungen in Mehrfach-Grafiken abgebildet werden. Die Aufteilung erfolgt dabei Anhand einer im Datensatz enthaltenen Variable, die zum Beispiel verschiedene Gruppen kennzeichnet.
Mit so einer Darstellung lassen sich mit sehr wenig Aufwand in den Daten enthaltene Teilaspekte (oder Facetten) sehr anschaulich visualisieren und zum Beispiel verschiedene Gruppen miteinander vergleichen. So lässt sich untersuchen, ob in den Daten enthaltene Muster bei verschiedenen Bedingungen gleich oder unterschiedlich sind.
Es gibt zwei Varianten des Faceting: Facet Warp und Facet Grid.
Facet Warp
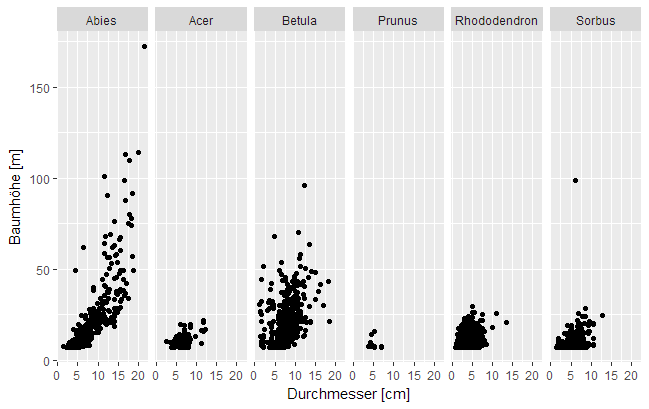
Facet Warp (in ggplot2 "facet_wrap()") wird für die nützlichere Variante gehalten (Wickham 2016: 17). Dabei wird ein langer Streifen mit Einzelbildern erstellt, der dann in eine zweidimensionale Anordnung umgebrochen wird. Aus einem Streifen mit vier Einzelbildern wird so zum Beispiel eine 2 x 2-Anordnung. Die Anzahl an Spalten und Zeilen kann dabei frei gewählt werden, auch eine einzeilige Darstellung ist möglich. Facet Wrap ist nützlich, wenn eine einzelne Variable viele Stufen (bzw. Gruppen) enthält und die Einzelabbildungen platzsparend angeordnet werden sollen.
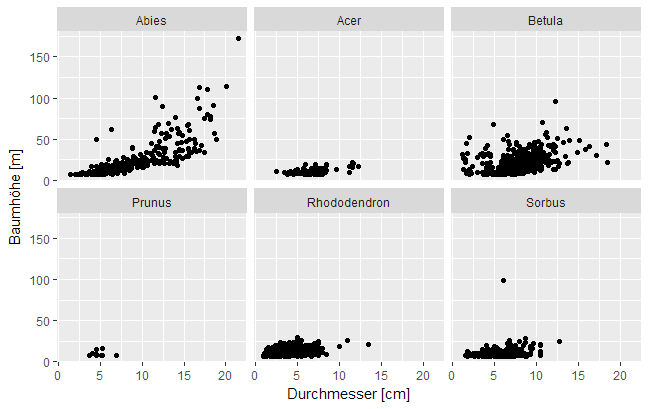
Abb. 3: Beispiel für eine ,,facet_wrap"-Abbildung, bei der die Beziehung zwischen Baumhöhe und -durchmesser getrennt für verschiedene Arten dargestellt wird.
Facet Grid
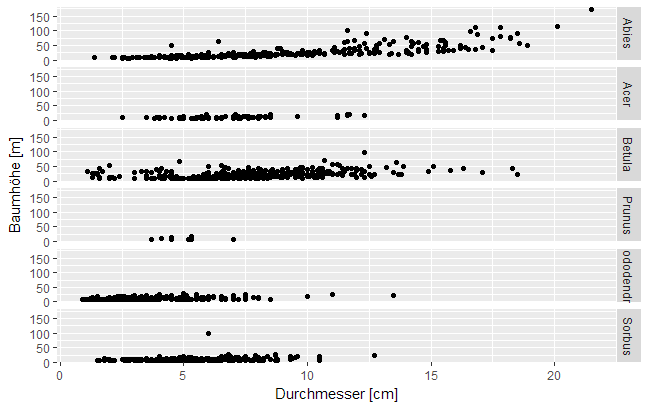
Auch Facet Grid (in ggplot2 "facet_grid()") ordnet Einzelbilder zweidimensional an. Dabei wird die Anordnung aber durch eine Formel definiert, die angibt, ob die Werte einer Variablen auf die Spalten oder Zeilen des ,,Rasters" der Mehrfachabbildung verteilt werden sollen. Die Verteilung über die Spalten erleichtert den Vergleich von y-Werten, da die vertikale Achse für alle Einzelbilder identisch ist. Die Verteilung über Zeilen erleichtert Vergleiche der x-Werte, da die horizontale Achse für alle Einzelabbildungen gleich ist. Damit ist diese Darstellung besonders nützlich, um Verteilungen zu vergleichen. Möglich ist auch die Aufteilung anhand zweier Variablen, bei der eine auf die Spalten und eine auf die Zeilen aufgeteilt wird.
Alternative: Gruppierung mit ästhetischen Eigenschaften
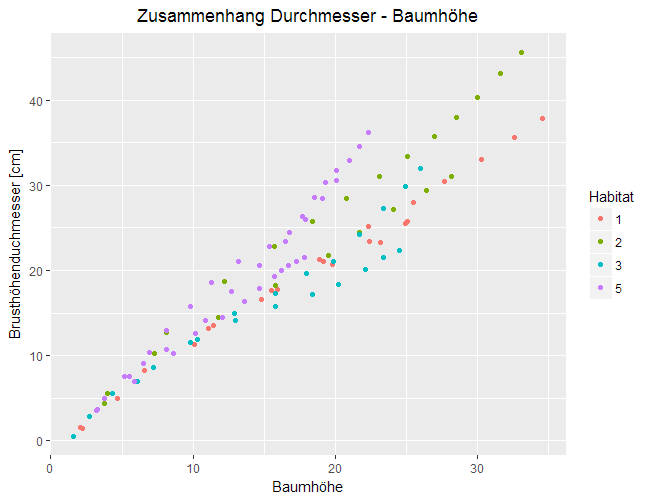
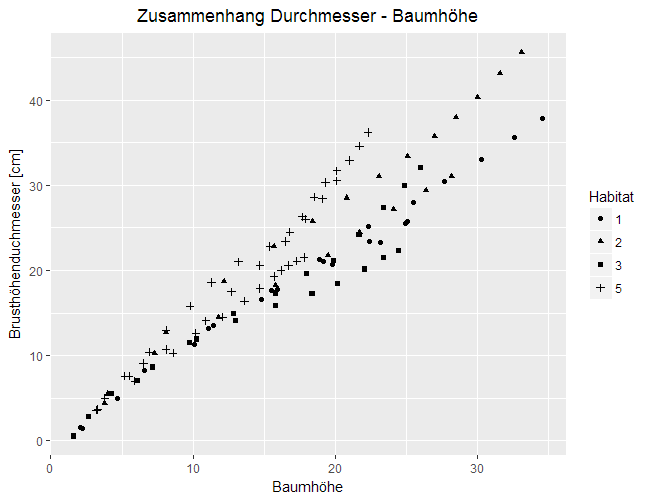
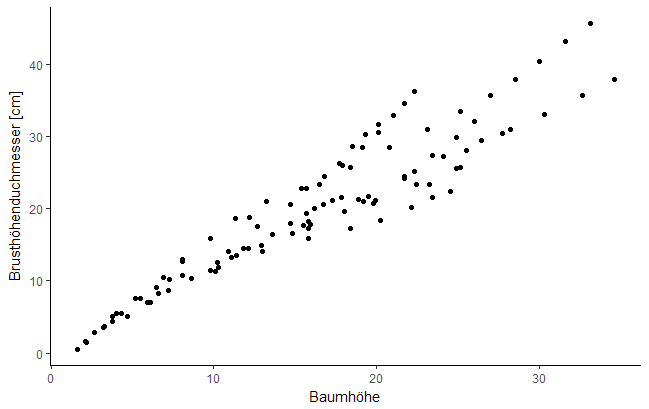
Eine Gruppierung von Daten ist auch mit den ,,ästhetischen Eigenschaften" möglich, zum Beispiel durch unterschiedliche Farben für Datenpunkte verschiedener Gruppen. Dabei werden die Datenpunkte alle in eine einzige Abbildung eingefügt, was das Erkennen kleiner Unterschiede erleichtert. Wenn die Gruppen stark überlappen, die Datenpunkte dicht beieinander liegen, kann hingegen Faceting die Differenzierung der Gruppen erleichtern. Beides hat Vor- und Nachteile und sollte je nach Datensatz und Fragestellung gegeneinander abgewogen werden.
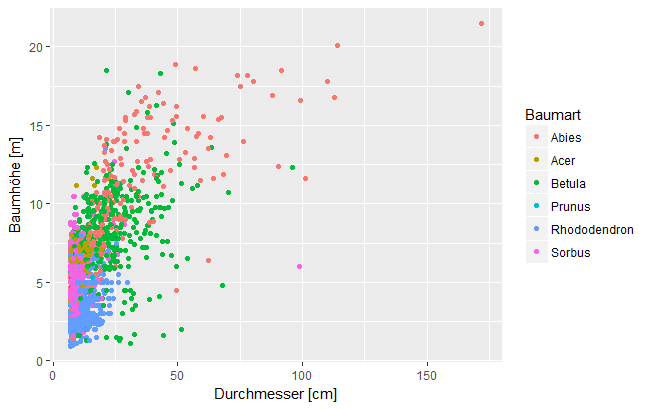
Abb. 4: Beispiel für eine Gruppierung mit aes()-Angabe bei geom_point() (... + geom_point(aes(colour = Baumart)) + ...), bei der die Beziehung zwischen Baumhöhe und -durchmesser getrennt für verschiedene Arten dargestellt wird.
Zusammenfügen von ggplot2-grafiken
Mit dem cowplot-Package lassen sich Einzelgrafiken zusammensetzen und ein besonderes, ,,publikationsbereites" Theme nutzen.
Karten mit ggplot2
ggplot2 unterstützt auch das Erstellen von Karten. Raster- und Vektordaten (Punkte, Linien, Polygone) lassen sich relativ einfach darstellen. Ausgangspunkt ist ein Dataframe mit den Daten. Zum Teil sind dabei Funktionen anderer R-Packages wie zum Bespiel raster oder sp erforderlich. Einen guten Überblick über das Erstellen von Karten mit ggplot2 geben Kapitel 3.7 in Wickham (2016) sowie folgende Online-Ressourcen:
Anderson, E. C. (2018). Making Maps with R. [letzter Aufruf 10.02.2019]
Grossenbacher, T. (2019). Beautiful thematic maps with ggplot2 (only). [letzter Aufruf 10.02.2019]
Wasser, L. (2019). Maps in R: R Maps Tutorial Using Ggplot. [letzter Aufruf 10.02.2019]
qplot() - schnelle Plots
Mit der Funktion qplot() (Quick Plots) lassen sich mit geringstem Aufwand, unter anderem sehr kurzem R-Code, einfach(ste) Abbildungen erstellen, ohne die "Grammatik" von ggplot2 im Detail zu beachten.
Bei der Verwendung von qplot() werden ein Datensatz und die ,,ästhetischen Eigenschaften" angegeben. qplot() wird dann darauf basierend sinnvolle geometrische Objekte und statistische Transformationen wählen. Die Funktion wird zum Beispiel ein Streudiagramm erstellen, wenn im Datensatz x- und y-Werte (also zwei Variablen) enthalten sind. Liegen hingegen nur x-Werte (eine Variable) vor, wird qplot() je nach Datentyp ein Histogramm oder ein Balkendiagramm erstellen.
Mit diesem Code wird zum Beispiel ein Streudiagramm erstellt:
qplot(bhd, hoehe, data = rol)
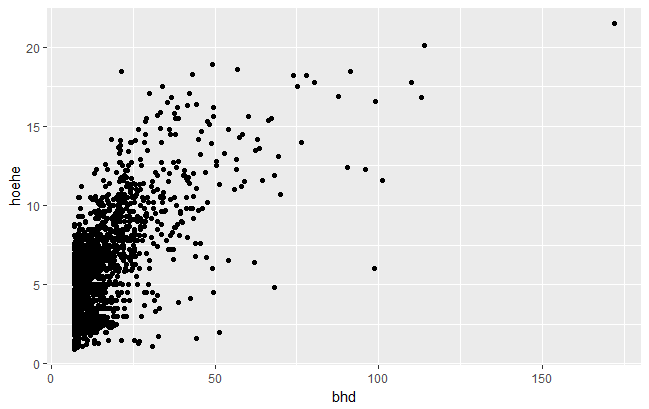
Abb. 5: Beispiel für ein mit der qplot-Funktion erstelltes Streudiagramm.
…. und so bei Angabe nur einer der beiden Variablen ein Histogramm:
qplot(hoehe, data = rol)
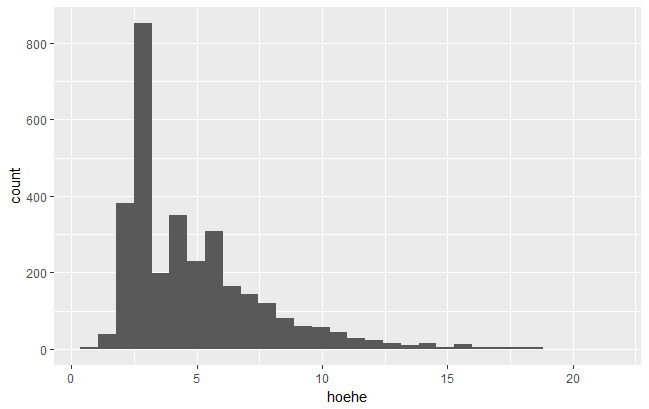
Abb. 6: Beispiel für ein mit der qplot-Funktion erstelltes Histogramm.
Bei der Verwendung von qplot() sollte folgendes Zitat beachtet werden:
"it [qplot] makes simple plots a little easier, but it doesn’t help with mastering the grammar" (Wickham 2016:viii).
Für die Erstellung komplexer Abbildungen mit verschiedenen ästhetischen Eigenschaften in unterschiedlichen Ebenen oder zum manuellen Einstellen von Eigenschaften sollte nicht qplot() sondern ggplot() verwendet werden.
Interaktive Grafiken und weitere Grafik-Packages in R
Interaktive Grafiken: ggvis
Mit ggplot2 lassen sich ausschließlich statische Grafiken erstellen. Es besteht keine Möglichkeit, diese interaktiv anpassbar zu gestalten. Wenn die ggplot2-Grafik erstellt wurde, ist sie nur durch Veränderung des Codes modifizierbar, nicht aber zum Beispiel durch Verstellen eines Schiebereglers auf einer Internetseite, die die Grafik anzeigt.
Das ist mit Grafiken, die mit dem R-Package ggvis erstellt wurden möglich: Abbildungen erstellen sich von alleine neu, wenn die zugrundelegenden Daten oder die Plot-Eigenschaften verändert werden. ggvis kann als gglot2-Nachfolge-Package angesehen werden. Die Funktionen von ggvis weiten die grundlegenden Ideen von ggplot2 aus, um interaktive Grafiken zu erstellen. Die Syntax ist ähnlich zu ggplot2, allerdings nicht 1:1 übertragbar, da ggvis komplett neu entwickelt wurde, auch um die Erfahrungen der Entwickler mit ggplot2 einfließen zu lassen. ggvis macht sich das R-Package shiny, mit dem interaktive Internetanwendungen erstellt werden können, zu Nutze und gibt Grafiken aus, die in einem Webbrowser, z.B. auch in RStudio, angezeigt werden können.
Weitere Informationen zu ggvis finden sich bei folgenden Quellen:
Weitere Grafik-Packages in R (Auswahl)
- dreidimensionale Grafiken (rgl)
- Netzwerk-Grafiken (und -Analyse) bzw. auf der Graphentheorie basierende Abbildungen (igraph)
- Datenvisualisierung für Statistik in den Sozialwissenschaften (sjPlot)
- Grafiken nach dem Trellis-Grafiksystem, mit dem Beziehungen zwischen Variablen, bedingt durch einen oder mehrere andere Variablen dargestellt werden können (lattice)
- plotrix
- gplots
Visualisierung mit R
Als Ausgangspunkt für weitere Informationen zu den Grafik-Möglichkeiten von R bietet sich die "Task View" Graphic Displays & Dynamic Graphics & Graphic Devices & Visualization des R-Netzwerks CRAN an.
Fragen oder Anmerkungen?
Für Anregungen und Kommentare zur Verbesserung dieses Digitalen Skripts ist das RLab-Team immer dankbar! Du kannst auch Fragen zu den Inhalten stellen! Nutze für all das gerne die Kommentar-Funktion!
Literatur
Zusätzlich zu den in diesem Digitalen Skript zitierten und für die Erstellung verwendeten Quellen sind einige weitere Ressourcen angegeben, die den Einstieg und die Arbeit mit ggplot2 erleichtern können.
Anderson, E. C. (2018). Making Maps with R. [letzter Aufruf 10.02.2019]
Chang, W. (2017). Cookbook for R: Graphs. [letzter Aufruf 10.02.2019]
Grossenbacher, T. (2019). Beautiful thematic maps with ggplot2 (only). [letzter Aufruf 10.02.2019]
Healey, K. (2019). Data Visualization: A Practical Guide. Princeton University Press. Princeton, USA. [Praxisnahe Einführung in das Erstellen von Abbildungen mit vielen ggplot2-Beispielen]
Institute for Quantitative Social Science (2018). R graphics with ggplot2 workshop notes. [letzter Aufruf 10.02.2019]
Kabacoff, R. I. (2017). Graphics with ggplot2. [letzter Aufruf 10.02.2019]
RStudio (2018). Data Visualization with ggplot2: Cheat Sheet 2.1.
Soltoff, B. (2018). Materials for class on the grammar of graphics and `ggplot2`. [letzter Aufruf 25.06.2019]
Wasser, L. (2019). Maps in R: R Maps Tutorial Using Ggplot. [letzter Aufruf 10.02.2019]
Wickham, H. (2010). A Layered Grammar of Graphics. Journal of Computational and Graphical Statistics 19:3–28 . doi: 10.1198/jcgs.2009.07098
Wickham, H. (2016). ggplot2: Elegant Graphics for Data Analysis. Springer International Publishing. Switzerland.
Wickham, H., Chang, W., Henry, L., Pedersen, T.L., Takahashi, K., Wilke, C., Woo, K., Yutani, H. (2019). Create a new ggplot. [letzter Aufruf 10.02.2019]
Wickham, H., Chang, W., Henry, L., Pedersen, T.L., Takahashi, K., Wilke, C., Woo, K., Yutani, H. (2019). Create Elegant Data Visualisations Using the Grammar of Graphics. [letzter Aufruf 10.02.2019]
Wickham, H., Chang, W., Henry, L., Pedersen, T.L., Takahashi, K., Wilke, C., Woo, K., Yutani, H. (2019). ggplot2 Function Reference. [letzter Aufruf 10.02.2019]
Wikipedia contributors (2019). Ggplot2. [letzter Aufruf 10.02.2019]
Wilkinson L. (2005). The grammar of graphics. Statistics and computing. Springer. New York, USA.
Literatur zum Thema ,,Datenvisualisierung", ohne direkten Bezug zu ggplot2:
Fischer-Stabel, P. (2018). Datenvisualisierung. UTB / UVK. München.
Tufte, E. R. (2015). The Visual Display of Quantitative Information. Graphics Press. Cheshire, Connecticut, USA. [Klassisches Buch zum Design statistischer Grafiken und Visualisierungen; siehe auch die Homepage des Autors]